「モーメントを使う問題がわからない」
「なぜモーメントを考えないといけないの?」
「モーメントの問題の解法が思いつかない」
このように思っている人は多いでしょう。
模試などで剛体の問題が出題されると、
すこし苦手意識を感じてしまう人も多いでしょう。
モーメントがやけに難しく感じるのは、
剛体の力学はそれまでの分野とは決定的な違いがあるからです。
ここではモーメントの解説をしますね。
この記事を読めば、
モーメントを考える意味が本質的に理解でき、
今まで持っていた苦手意識が吹き飛びます。
ぜひ最後まで読んでみてください。
「質点の力学」と「剛体の力学」とは?
これまで位置・速度・加速度の計算、
運動方程式の取り扱い方などなど、
運動の法則を勉強してきました。
これまでの知識を使えば、
物体がどのような軌道で運動するかを、
数式で計算することができます。
しかし、現実はこうも簡単ではありません。
今までは物体をすべて、
質量はあるけど体積は持たない点である、
「質点」として捉えてきました。
でも実際の物体には体積があり、
体積がある現実の物質は回転することができます。
野球でカーブやフォークを投げると、
最初は同じ軌道でも途中で曲がってしまうように、
回転が起こると「質点の力学」からずれてしまうのです。
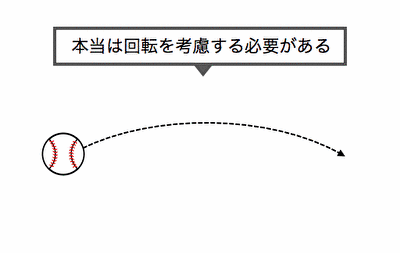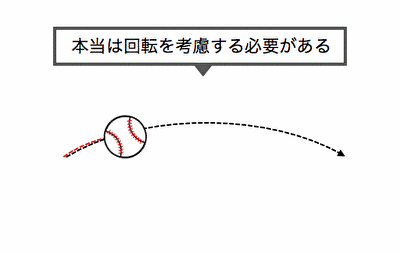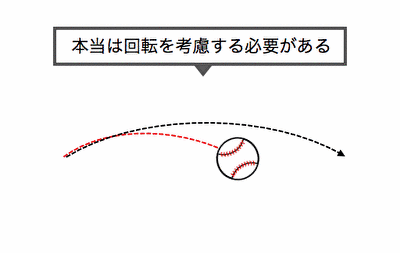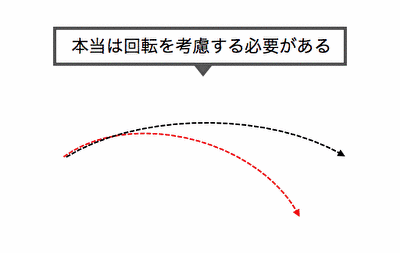
現実の物体のように、
質量も体積も持つ物体を「剛体」といいます。
上の例からもわかるように、
「剛体の力学」では今までの運動に加えて、
回転の影響を考慮する必要があるのです。
そして高校物理の剛体の力学の分野は、
回転の影響の考え方の基礎を勉強する分野です。
物体の位置を求める今までとは違い、
物体の回転を取り扱う別分野なのです。
まずはこれをしっかりと認識しておきましょう。
モーメントは回転を扱う
それでは剛体の力学特有である「回転」は、
物理的にはどのように考えるのでしょうか。
この回転を取り扱うための道具が「モーメント」です。
モーメントの具体的な定義の前に、
モーメントの考え方のイメージを共有しておきましょう。
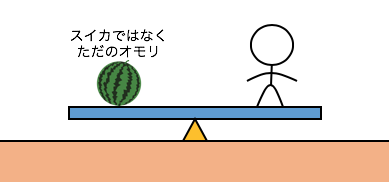
シーソーの片方にオモリがあって、
反対側に人間が乗ることで持ち上げる、
という場面を考えましょう。
シーソーの根元に乗るよりも、
できるだけ端の方に乗った方が、
シーソーが傾きやすそうですよね。
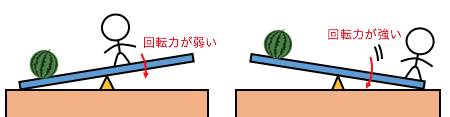
この例で言うならば、
端に乗る方がシーソーを回転させる力が強かった、
つまりモーメントが大きかったと言うことです。
これがモーメントのイメージです。
以上のイメージを元に、
モーメントの定義を考えていきましょう。
モーメントの定義
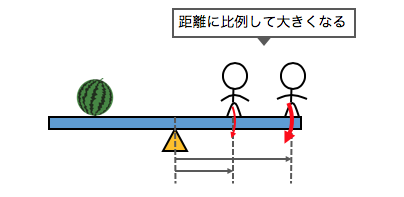
シーソーに力が働いているとき、
回転の中心から距離が離れるほど、
回転の勢いは激しくなりそうです。
これを考えると、
モーメントは中心からの距離に比例しそうです。
また画像では上向きに力が働いていますが、
仮に右向きに力が働いたとしても、
回転が起こることはありません。
別の言葉で言うなら、
回転方向の力だけがモーメントに影響しそうです。
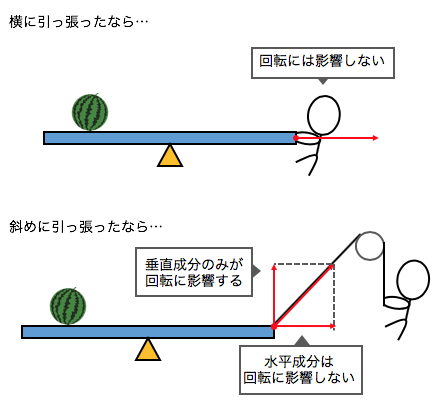
以上を踏まえれば、
モーメントの定義は以下のようになります。
点Oまわりのモーメント\(M\)は、距離\(l\)と力\(F\)によって、\(M=lF\)と表される。ただし\(l\)は点Oから作用点Pまでの距離、\(F\)は直線OPに垂直な力である。
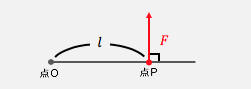
定義自体はイメージ通りではないでしょうか。
また上の定義から分かる通り、
モーメントは回転中心Oを決めることで、
「点Oまわりのモーメント」として定義されます。
回転中心とは呼んだものの、
この点Oは自分で好き勝手に選んでいいです。
これは具体例を見ないとわかりづらいので、
細かい説明は後に回します。
モーメントの計算
具体的な例で実際にモーメントを計算してみましょう。
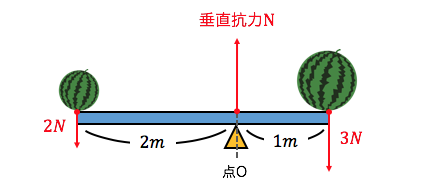
図に書き込んだ点Oを中心とすると、
右側の物体Aは点Oに対して時計回りの向きに、
左側の物体Bは点Oに対して反時計回りの向きに、
力が働いています。
またモーメントの大きさはそれぞれ、
物体A:\( M_{A} = 1.0[m]×3.0[N] = 3.0[N\cdot m] \)
物体B:\( M_{B} = 2.0[m]×2.0[N] = 4.0[N\cdot m] \)
となります。
ちなみに点Oにも垂直抗力が働きますが、
中心からの距離が0の点に働くので、
\(M_{O}=N×0=0\)となりモーメントはありません。
以上から、時計回りの向きに3.0[N・m]、
反時計回りの向きに4.0[N・m]の、
モーメントがかかっているとわかりました。
剛体の釣り合いの条件
モーメントが求められるようになったので、
次に「剛体の釣り合いの条件」を考えましょう。
質点の釣り合いの条件は、
力の釣り合いが成り立っていればよいのでした。
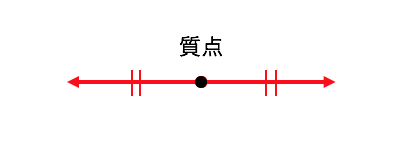
剛体であってもこれは変わりません。
力が釣り合わなければ動いてしまいます。
ただ以下の例はどうでしょうか。
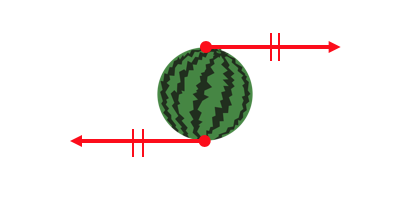
確かに力は釣り合っていますが、
明らかに回転運動が起こってしまいそうですね。
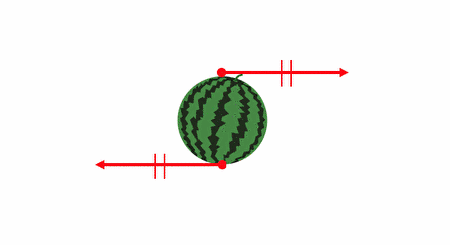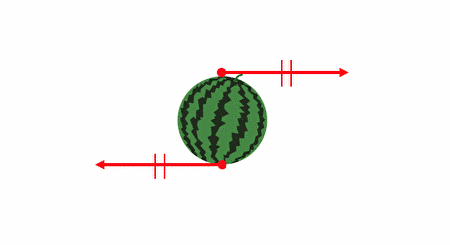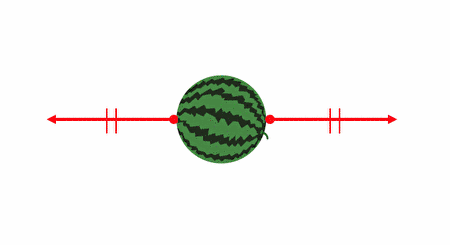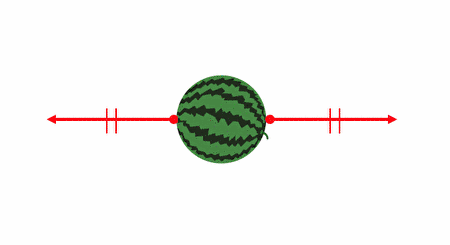
つまり、剛体が釣り合うのは、
・力の釣り合い
・モーメントの釣り合い
が同時に満たされるときです。
剛体が静止するためには、
この2つの条件を確かめればいいのですね。
練習問題
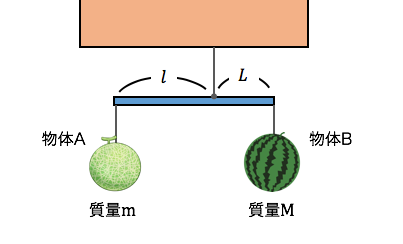
それでは早速、解答にうつります。
まずは力の図示をしましょう。
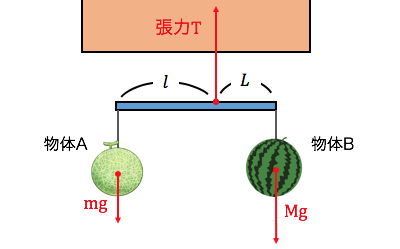
この状態だと少し見にくいので、
最低限必要な情報だけにすれば、
以下のようになります。
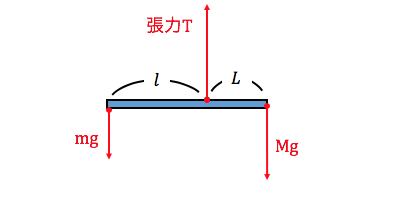
張力の作用点を中心に、
それぞれの力が生み出すモーメントを計算しましょう。
物体Aは、反時計回りの向きに\(l\cdot mg\)、
物体Bは、時計回りの向きに\(L\cdot Mg\)、
張力は基準点上なので\(0\cdot T=0\)です。
必要な情報が集まったので、
剛体の釣り合いの条件を考えます。
力の釣り合い:\(T=mg+Mg\)
モーメントの釣り合い:\(L\cdot Mg=l\cdot mg\)
これを解けば、
\[ M = \frac{l}{L}m \]
このようにしてMが求まりました。
剛体の釣り合いでは、
今まではなかったモーメントの釣り合いも必要なので、
ぜひ問題集で練習しておいてください。
力の釣り合い:\(T=mg+Mg\)
モーメントの釣り合い:\((l+L)\cdot Mg=l\cdot T\)
後者の式に前者を代入して、
\begin{align*}
(l+L)\cdot Mg&=l\cdot (mg+Mg) \\
L\cdot Mg&=l\cdot mg \\
M &= \frac{l}{L}m \\
\end{align*}
逆に言えば、基準点の決め方を工夫すると計算がラクになる場合があるとも言えます。
補足:剛体の力学
ここまでの話を簡単に復習しながら、
剛体の力学について補足の説明をします。
今まで考えてきた「質点の力学」に対して、
体積がある剛体を扱う「剛体の力学」では、
物体の回転運動に着目する必要があります。
質点の運動では力によって運動が変化しましたが、
回転運動では「モーメント」によって運動が変化します。
質点の運動では、
力の釣り合い→運動方程式と派生することで、
質点の運動を予測することができましたね。
一方で剛体の回転運動は、
高校ではモーメントの釣り合いまでしか習いません。
回転運動の運動方程式的なものは、
大学に入ってから勉強します。
教科書などでは、
質点の力学の合間に急にモーメントが現れ、
なんとなく混乱してしまう生徒もいます。
以上の対比関係を理解していると、
少し頭が整理されるのではないでしょうか。
まとめ
今回は剛体の力学の中の、
モーメントとその釣り合いの解説でした。
モーメントのイメージを使うには、
まずは「回転運動を扱っている」と、
明確に意識しておくことが大切です。
その上で定義をきちんと理解しておきましょう。
ただしモーメントの問題では、
練習問題でも少し言及した基準点の取り方で、
混乱してしまう場合が多いです。
その辺りはぜひ問題演習を重ねて、
克服していってください。













コメントを書く