単振動では様々な「公式」が出てきます。
それらを全てまとめると以下の通り。
変位 \(x=Asin(\omega t+\alpha)\)
速度 \(v=A\omega cos(\omega t+\alpha)\)
最大値は\(A\omega\)
加速度 \(a=-A\omega^{2} sin(\omega t+\alpha)\)
最大値は\(A\omega^{2}\)
単振動の周期
\begin{align*}
&\omega T = 2\pi \\
&T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}}
\end{align*}
単振動の位置エネルギー\[ 位置エネルギー=\frac{1}{2}kx^2\]
あなたはこれらをただただ丸暗記していませんか？
これらの数式の意味を理解せず、
機械的に丸暗記をしていては、
単振動どころか力学すら得意にはなれません。
ここでは単振動について、
本質的な知識や考え方を伝えていきますね。
この記事を最後まで読むことで、
単振動がなぜ難しいのかを理解することができ、
そして単振動を得意科目にできるでしょう。
単振動は力学の中でも出題率が高く、
単振動ができる＝物理で高得点を狙っていけます。
ぜひ読み飛ばさずに読んでみてください。
力学の最難関！単振動とは？
「単振動」とは、
バネが伸び縮みしながら振動したり、
振り子がゆらゆらと揺れるような運動です。
単振動する物体は、
サインカーブを描きながら振動します。
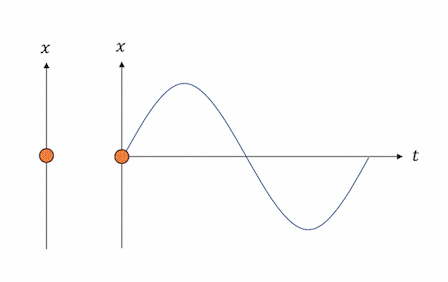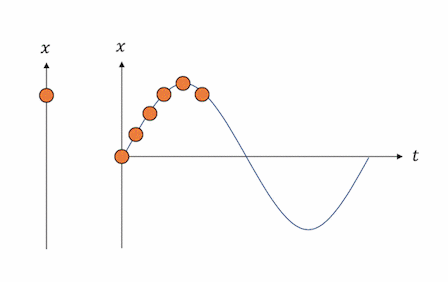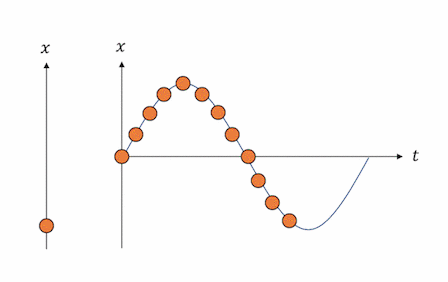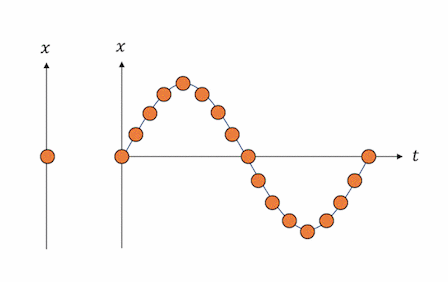
「波動」の分野を勉強した人なら、
なんとなく波のようにも見えますね。
では単振動がどんなときに発生するかというと、
物体に以下のような力がかかる場合です。
\begin{align*}
F = -kx (復元力) \\
ただしxは変位、kは定数
\end{align*}
この力を日本語で言うなら、
前に進むほど後ろに引っ張られ、
後ろに進むほど前に引っ張られる力、
です。
物体が移動しようとしても、
常に元の位置に「復元」されてしまう、
そんな状況のときに単振動が起こります。
さて、では力が表せるのならば、
運動方程式で加速度が求まり、
加速度から物体の変位xが求まるはずです。
\begin{align*}
ma &= -kx \\
a &= -\frac{k}{m}x
\end{align*}
しかし、ここで問題が生じます。
一見、加速度が求まったようですが、
この式からは「ある理由」で位置が求まりません。
この式を解くためには大学の数学が必要で、
結果的には以下のように式変形されます。
\begin{align*}
a &= -\frac{k}{m}x \\
x &= Asin(\sqrt{\frac{k}{m}}t+\alpha)
\end{align*}
何が起こったんだ！？
と思いますよね 笑
実はここで大学数学が必要で、
急に意味不明に三角関数が出てくるから、
単振動は難しく感じるのです。
「ある理由」とはなんなのか、
どんな式変形をしたらxが求まったのか、
についてはこの記事の最後に解説します。
ただしそこまで理解する必要もないので、
多くの人はx=…の式を覚えてしまえばいいでしょう。
ここからはx=…の意味の説明と、
そこから求まる単振動の公式を学んでいきます。
単振動の変位・速度・加速度
先ほど求めたように、
単振動の変位xは以下のように表せます。
\begin{align*}
x &= Asin(\sqrt{\frac{k}{m}}t+\alpha) \\
&= Asin(\omega t+\alpha) (\omega = \frac{k}{m}とする)
\end{align*}
ただし、
振幅Ａ 単振動の揺れの大きさ
初期位相α 振動のスタート位置のずれ
角周波数ω 1秒あたりの位相の変化
A、αは初期条件によって決まり、
ωはkとmによって決まります。
なぜこのように表せるのかは、
高校レベルでは少し難しいので、
この記事の最後に応用として説明します。
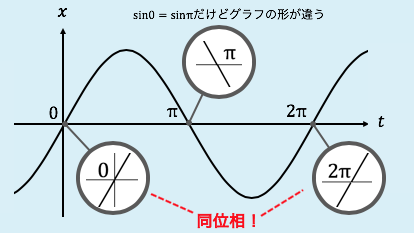
簡単に言えば三角関数の角度の部分です。ただ、例えば\(\mathrm{sin0}\)と\(\mathrm{sin2\pi}\)では、グラフの形が全く同じですよね。これを「位相が同じ(同位相)」と言い、角度が違ってもグラフが一緒なら位相は等しくなるとわかります。
次に変位を使って速度と加速度を求めましょう。
速度と加速度については、
以下で本質的に解説しているので、
まだ呼んでいない人はそちらからご覧ください。
【合わせてチェック】
・超重要！位置・速度・加速度を理解しよう！【高校物理】
速度とは、位置xを時間tで微分したもの、
加速度とは、速度を時間tで微分したものでしたね。
これを使えば以下のように計算できます。
\begin{align*}
v &= \frac{dx}{dt} = A\omega cos(\omega t+\alpha) \\
a &= \frac{dv}{dt} = -A\omega^{2} sin(\omega t+\alpha) = -\omega^{2}x
\end{align*}
加速度の計算では、
途中で\(x=Asin(\omega t+\alpha)\)の形が出てきたので、
xを代入しました。
sinもcosも最大値は1なので、
速度の最大値は\(A\omega\)、加速度の最大値は\(A\omega^{2}\)、
となることもすぐにわかりますね。
以上をまとめると以下のとおりです。
変位 \(x=Asin(\omega t+\alpha)\)
速度 \(v=A\omega cos(\omega t+\alpha)\)
最大値は\(A\omega\)
加速度 \(a=-A\omega^{2} sin(\omega t+\alpha)\)
最大値は\(A\omega^{2}\)
単振動の周期
単振動は、周期的に振動を繰り返します。
周期は位相が同じになるごと、
つまりsinの中身が2πずれるごとです。
よって周期Tは、
\begin{align*}
\omega T &= 2\pi \\
T &= \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}}
\end{align*}
となります。
少し実践的な考え方も紹介しておきます。
単振動の運動方程式を考えると、
\begin{align*}
ma &= -kx \\
a &= -\frac{k}{m}x \\
&= -\omega^{2}x \\
(\omega&=\sqrt{\frac{k}{m}}を用いた)
\end{align*}
となります。
つまり、ある問題で普通に力を図示し、
運動方程式を立てて
\[ a = -◯x \]
の形になった場合、
周期は以下のように計算できます。
\begin{align*}
\omega^2 &= ◯ \\
T &= \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{1}{◯}}
\end{align*}
つまり周期を求める問題では、
運動方程式を書いてωを求めれば、
簡単に周期がわかるということですね。
単振動の位置エネルギー
「エネルギー」とは、
「仕事」と表裏一体の概念で、
仕事をされたならその分エネルギーが溜まっていると考えます。
仕事に関しては、
以下で詳しく解説しています。
【合わせてチェック】
・仕事とエネルギーを解説！定義から正しく理解しよう
ここでは簡単に、
単振動の位置エネルギーを確認しておきます。
バネ定数kのバネにくっついた物体が、
変位xの位置にあるとすると、
これを外力で動かすにはkxの力が必要です。
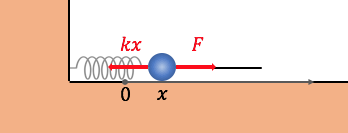
このようにして変位0からxまで引っ張るとき、
最初はk×0=0[N]で引っ張ることができますが、
徐々に徐々に必要な力が大きくなります。
これをグラフに書いたのが以下です。
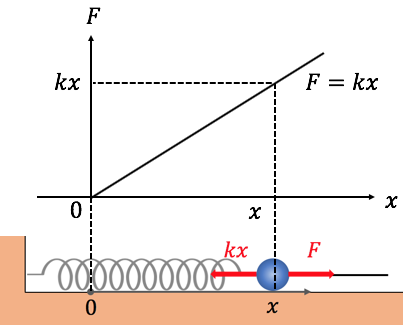
最初の方は小さい仕事で済むけど、
引っ張るほど必要な仕事が大きくなる、
これを考慮すると必要な仕事はグラフの面積になります。
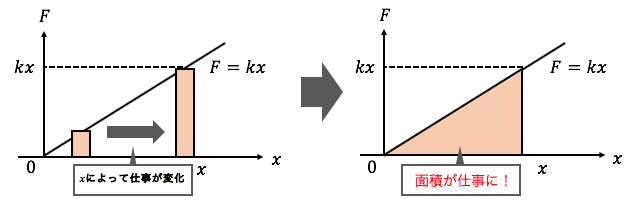
よって必要な仕事は、
\[W = \frac{1}{2}kx\times x =\frac{1}{2}kx^2 \]
となり、これが単振動の位置エネルギーになります。
もしくは仕事の定義に基づくなら、
\[ W = \int_{0}^{x}Fdx’ \]
だから、F=kxを代入すれば、
\begin{align*}
W &= \int_{0}^{x}Fdx’ \\
&= \int_{0}^{x}kx’dx’ \\
&= \frac{1}{2}kx^2 \\
\end{align*}
となります。
応用：微分方程式による解法
一番最初に、
\(a = -\frac{k}{m}x\)
の式が「ある理由」で解けないと言いました。
ここでは物理が得意な人向けに、
その理由について解説していきます。
興味がない人はスキップして大丈夫です。
さて、まずは加速度aの定義を思い出すと、
加速度は変位xの時間の二階微分でした。
つまり先ほどの式は、
\[a = \frac{d^2x}{dt^2} =-\frac{k}{m}x\]
とかけます。
ここで数2で習った積分を思い出しましょう。
普通積分をしたければ、
\(\frac{dx}{dt}=t\)→\(x=\frac{1}{2}t^2+C\)のように、
\(\frac{dx}{dt}=tの関数\)となるはずです。
しかし今回はなんと、
右辺にxが混ざってしまっています。
これは簡単に言えば、
普段は\(y’=x\)などしか扱わないのに、
今回は\(y’=y\)という形が出てきたイメージです。
数2ではこんな積分習いませんでしたね。
このように\(y’\)と\(y\)が混ざったり、
\(\frac{dx}{dt}\)と\(x\)が混ざったりして、
関数とその微分が混ざったものを微分方程式と呼びます。
微分方程式の解法に従えば、
\(\frac{d^2x}{dt^2} =-\frac{k}{m}x\)の解は以下のようになります。
\begin{align*}
x &= Asin\sqrt{\frac{k}{m}t} + Bcos\sqrt{\frac{k}{m}t} \\
&= \sqrt{A^2+B^2}sin(\frac{k}{m}t+\alpha) \\
&= Asin(\frac{k}{m}t+\alpha) \\
(&\sqrt{A^2+B^2}→Aと置き直した)
\end{align*}
微分方程式さえ使えれば、
単振動も運動方程式を使って解けますが、
微分方程式が使えないことによって、
単振動では暗記が多く思えてしまうのです。
ここまで読んでくれたあなたは、
「単振動も本当はただの運動方程式なんだ」
と思えるといいですね。
まとめ
今回は単振動に関する、
さまざまな数式を確認しました。
以下にもう一度まとめておきましょう。
変位 \(x=Asin(\omega t+\alpha)\)
速度 \(v=A\omega cos(\omega t+\alpha)\)
最大値は\(A\omega\)
加速度 \(a=-A\omega^{2} sin(\omega t+\alpha)\)
最大値は\(A\omega^{2}\)
単振動の周期
\begin{align*}
&\omega T = 2\pi \\
&T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}}
\end{align*}
単振動の位置エネルギー\[ 位置エネルギー=\frac{1}{2}kx^2\]
変位の式さえ覚えてしまえば、
その他の式は暗記する公式ではありません。
ぜひきっちりと理解しておいてください。
