位置を求めるというのは、
力学の最終目標です。
全瞬間の位置を求めることができれば、
物体が動く通り道を全て予測できるからですね。
そして位置を求めるためには、
速度や加速度の概念が必要不可欠です。
しかしこんなに重要なのに、
速度や加速度を本質的に理解している受験生は少ないです。
そこで今回は速度・加速度の解説記事です。
この記事を理解することで、
速度・加速度を本質的に理解することができ、
この先の力学の勉強がスムーズに進みます。
ぜひ最後まで読み飛ばさずに読んでみてください。
目次
位置・速度・加速度とは?
速度 単位時間あたりの位置の変化率
加速度 単位時間あたりの速度の変化率
「位置」というのは、
物体がどこにあるかを表す量です。
そして力学という学問は、
位置の変化を調べて運動を予言する学問です。
どういうことかというと、
時間ごとの位置の変化がわかれば、
物体の運動の軌跡がわかるということです。
だから位置を調べることは、
力学の中心テーマなのですね。
そして位置を調べるために、
時間あたりの位置の変化具合である「速度」と、
時間あたりの速度の変化具合である「加速度」も、
とても重要です。
今回は速度、加速度の意味と定義を、
一緒に確認していきましょう。
速度の意味・定義
速度の意味を思い出すと、
一定の時間の間にどれだけ位置が変化したか
でした。
だから一定の時間\(\Delta t\)秒の間に位置が\(\Delta x\)だけ変化すると、
そのときの速度\(v\)は、
\[ v = \frac{\Delta x}{\Delta t} \]
\(\Delta t = 5\)秒間に\(\Delta x = 10\)m進んだとしたら、
速度は2m/sになるのと同じ計算です。
ただしこれは「平均の速度」になっています。
例えば5秒間で10mといっても、
1秒目は動き出したばっかりでゆっくり、
5秒目には勢いがついて素早く動いたかもしれません。
できれば車の速度メーターのように、
今この瞬間どれくらいの速度かを知りたいですよね。
このような「瞬間の速度」を求めるためには、
\(\Delta t=0.00…01\)秒という短時間の位置変化を考えればよく、
以下のように計算することができます。
\[ v = \lim_{\Delta t \to 0}\frac{\Delta x}{\Delta t} = \frac{dx}{dt}\]
このように速度というのは、
位置が時間によってどのくらい変化するか、
という「位置の時間微分」で表せます。
最初は難しいかもしれませんが、
説明の流れをなんとなく理解しておきましょう。
速度から位置を求めてみよう
先ほどは位置から速度を考えましたが、
次は逆に速度から位置を計算してみます。
まずは簡単な具体例から。
車がずっと同じスピード\(v\)で走ったとしましょう。
これをv-tグラフで書くとこんな感じです。
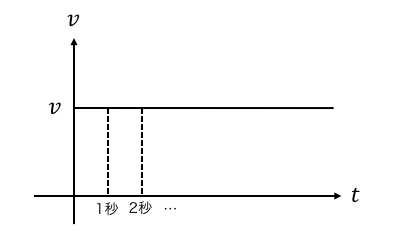
最初の1秒の間にv[m]進み、
1秒〜2秒の間にもv[m]進み、…
と進んでいるので、
\(t\)秒後の位置\(x\)は、
\[ x = vt \]
となります。
ではもし車の速度が一定ではなく、
アクセルを踏んだりブレーキを踏んだりしたらどうなるでしょうか。
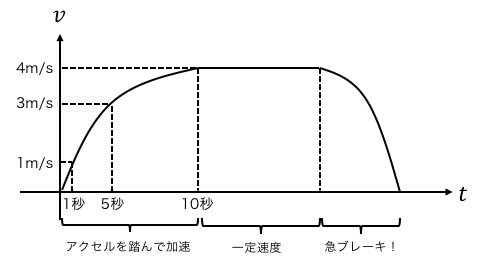
最初の1秒は1m/s×1秒=1mくらい、
途中の5秒は3m/s×1秒=3mくらい、
途中の10秒は4m/s×1秒=4mくらい進みます。
そして結果的に進んだ距離は、
これらの足し算になります。
その結果以下の図のように、
v-tグラフの面積が進んだ距離になるのです。
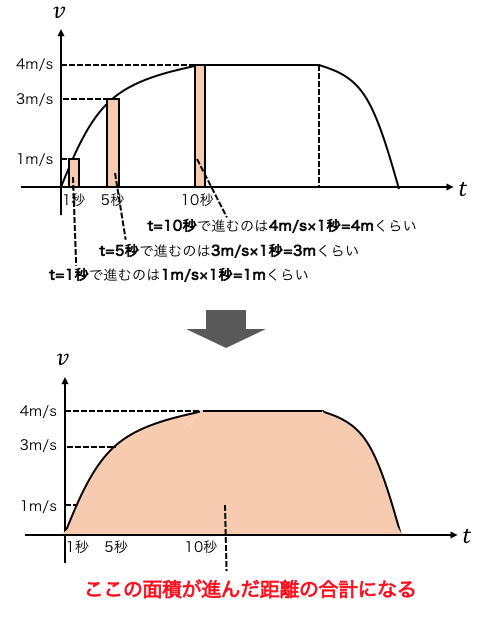
よって速度がわかれば、
以下のように位置を計算することができます。
ある時刻\(t_{0}\)・位置\(x_{0}\)からスタートし、速度が\(v(t)\)(時間の関数)であるとき、時刻\(t\)での位置\(x\)は以下のように計算できる。
\[ x = x_{0} + \int^{t}_{t_{0}}v(t)dt \]
こちらもこれだけ聞いても、
なかなか理解は難しいと思います。
参考書などで問題を解きながら、
少しずつ理解していきましょう。
加速度の意味・定義
速度が理解できれば、
加速度も同じように理解できます。
速度が位置の時間変化だったのに対し、
加速度は速度の時間変化ですから、
以下のように定義できます。
\[ a = \lim_{\Delta t \to 0}\frac{\Delta v}{\Delta t} = \frac{dv}{dt} = \frac{d^{2}x}{dt^{2}}\]
さらに加速度から速度を計算することもできます。
ある時刻\(t_{0}\)・速度\(v_{0}\)からスタートし、加速度が\(a(t)\)(時間の関数)であるとき、時刻\(t\)での速度\(v\)は以下のように計算できる。
\[ v = v_{0} + \int^{t}_{t_{0}}a(t)dt \]
こちらに関しても、
加速度が積み上がって速度になる、
というイメージが持てるといいですね。
高校で習う公式を確認しよう
高校の力学の授業で、
こんな公式たちを学びましたよね。
等速運動 &x = x_{0} + vt \\
&\\
等加速度運動 &v = v_{0} + at \\
&x = x_{0} + v_{0}t + \frac{1}{2}at^{2}
\end{align*}
速度・加速度の意味を理解していないと、
あ、加速度運動なのに等速運動の公式使っちゃった…
というようなミスが出てきます。
今回の記事で学んだことを使い、
授業で習った公式を確認していきます。
①等速運動
等速運動とは、速度\(v\)が一定ということですね。
v-tグラフの面積を思い出してもいいですし、
積分での方法を思い出してもいいですが、
時刻0からスタートしたとすれば、
x &= x_{0} + \int^{t}_{0}vdt \\
&= x_{0} + vt
\end{align*}
となります。
②等加速度運動
等加速度運動とは加速度\(a\)が一定ということです。
こちらも定義通り計算してみましょう。
v &= v_{0} + \int^{t}_{0}adt \\
&= v_{0} + at \\
x &= x_{0} + \int^{t}_{0}vdt \\
&= x_{0} + v_{0}t + \frac{1}{2}at^{2}
\end{align*}
応用:単振動の位置と速度
バネを引っ張ると逆向きに力が働き、
元の位置に戻るために振動します。
このような動きを「単振動」といいます。
単振動の位置\(x\)は、
\begin{align*}
x&=Asin\omega t \\
(&ただしAは振れ幅、ωは定数)
\end{align*}
となることがわかっています。
つまり単振動の速度\(v\)は、\begin{align*}
v &= \frac{d}{dt}Asin\omega t\\
&= A\omega cos\omega t
\end{align*}
となります。
(三角関数の微分は数3で習います)
ときどき、
速度の公式といえば\(v=v_{0}+\frac{1}{2}at^{2}\)、
のように思ってしまう人がいますが、
実際は三角関数が速度になることだってあるのです。
以上、速度と加速度の公式を
勘違いしないための補足でした。
まとめ
位置・速度・加速度の関係をもう一度まとめておきます。
v &= \lim_{\Delta t \to 0}\frac{\Delta x}{\Delta t} = \frac{dx}{dt} \\
x &= x_{0} + \int^{t}_{t_{0}}v(t)dt
\end{align*}
加速度の定義式\begin{align*}
a &= \lim_{\Delta t \to 0}\frac{\Delta v}{\Delta t} = \frac{dv}{dt} = \frac{d^{2}x}{dt^{2}} \\
v &= v_{0} + \int^{t}_{t_{0}}a(t)dt
\end{align*}
この記事で言いたいのは、
微分と積分で力学を考えろではなく、
速度は位置の瞬間の変化量なんだよ、
位置は速度の積み重ねの結果なんだよ、
ということです。
これらがイメージできると、
力学の理解が格段に上がるでしょう。














コメントを書く