高校化学第一の難関、「モル計算」。
多くの高校生がここでつまずき、
化学が苦手になってしまいます。
あなたもモル計算に苦手意識はありませんか?
モル計算に苦手意識を持ってしまうのは、
物質量の意味を正確にイメージできておらず、
そのせいで「計算の型」ができていないからです。
ここではモル計算を本質的に説明していきます。
ここの内容を練習しておくことで、
「モル」がなんのためにあるのかが明確に理解でき、
モル計算で手が止まることはなくなるでしょう。
この記事の最後には例題や練習問題もあり、
理解の助けになると思います。
ぜひ最後まで読んでみてください。
物質量とは
化学で扱う物質は原子という小さい粒が
集まることでできています。
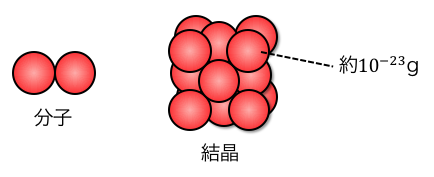
この原子1個の質量は約10-23gで、
それが約1023個集まることでやっと1gの物質ができます。
これでは化学の計算がとっても大変です。
そこで原子をいくつかまとめて、
「1箱に詰める」ことで扱いやすくしたのが、
「物質量(mol)」という考え方です。
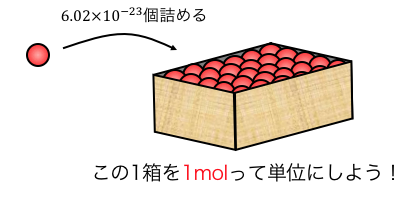
鉛筆をこまごま数えていたら面倒だから、
1ダース=12本とまとめているのと同じですね。
原子もこまごま数えていたら大変なので、
1mol=6.02×1023個とまとめて考えるわけです。
molと言われると難しいものに感じますが、
ただ原子を箱詰めにして数えてるだけで、
本質は個数と変わらないのですね。
1.9926×10-23[g/個]×6.02×1023[個]≒12g
となり、「炭素の原子量[g]」となっていますね。これが計算を楽にしてくれます。
【合わせてチェック】
・相対質量・原子量・分子量・式量、理解できてる?
物質量と粒子数・質量・体積の関係
物質量(mol)を考えることで、
こまごま原子を数えずにまとめて扱えるようになりました。
次に物質量と他の化学量の関係を見ていきます。
物質量から質量や体積など変換できれば、
「物質量さえわかればなんでもわかる!」
となってうれしいですからね。
それでは順番に見ていきましょう。
物質量と粒子数の関係
そもそも物質量は、
6.02×1023個をまとめて1molとする
というのが定義でした。
つまり物質量と粒子数は定義通りですね。
1molで6.02×1023個であることを6.02×1023個/molと
表現し、これを「アボガドロ定数」と呼びます。
物質量と質量の関係
6.02×1023個って微妙な数字ですよね。
実はこれは、炭素原子を6.02×1023個集めたら、
質量が原子量の数字と同じ12gになるように作られています。
そのようにすれば、
原子量23のナトリウムを1mol集めれば23gだし、
分子量18の水を1mol集めれば18gだし、
式量58.5の塩化ナトリウムを1mol集めれば58.5gになります。
1mol集めれば質量が原子量・分子量・式量に一致するのです。
この「1molで何gになるか」を「モル質量」といい、
モル質量は原子量・分子量・式量にg/molをつけたものです。
物質量と体積の関係
すべての理想気体1molは標準状態で、
気体の種類に関係なく22.4Lになります。
1molで22.4Lになることは22.4L/molと表現します。
物理的な難しい話を無視して考えやすくしたものが「理想気体」です。例えば気体ごとに分子の大きさは違うけど、理想気体では全て大きさ0として考えています。
「標準状態」とは、0℃、1013hPaの状態を指します。例えば温度が上がれば気体は膨張してしまいそうですが、標準状態に合わせればいつも22.4Lだということです。
モル計算の例題
物質量の意味、各量への変換がわかったところで、
実際に計算をしてみましょう。
化学の計算の基本は、
①まずはmolに直す
②化学反応などはmolで考える
③最後にmolから求めたい量に変換する
です。
では例題を解いてみましょう。
(1)0.50molの粒子は何個か。
(2)3.0×1024個の粒子は何molか。
(3)酸素分子1.5×1023個は標準状態で何Lか。
(1)0.50molの粒子は何個か。
今回は最初からmolが与えられ、
個数を知りたいだけなので③を考えれば良さそうです。
\[
\mathrm{ 0.50mol \times \frac{6.0\times 10^{23}個}{1mol} = 3.0\times 10^{23}個}
\]
後半の分数は単位である[個/mol]で、
「1molで6.0×1023個」
というのを数式にした形です。
これによって単位molが約分されて、
答えの単位が個になっています。
(2)3.0×1024個の粒子は何molか。
これはmolに直すだけの問題なので
①を考えればいきなり答えになります。
\[
\mathrm{ 3.0×10^{24}個 \times \frac{1mol}{6.0\times 10^{23}個} = 5.0mol}
\]
こちらもやはり、
「6.0×1023個で1mol」
というのを数式にしています。
言葉を数式に変えて、単位を変換していけば、
自然に答えに辿り着けますね。
(3)酸素分子1.5×1023個は標準状態で何Lか。
1.5×1023個とか言われても…
って感じなのでまずはmolにまとめてあげましょう。
\[
\mathrm{ 1.5×10^{23}個 \times \frac{1mol}{6.0\times 10^{23}個} = 0.25mol}
\]
molにしてしまえば何にでも変換できます。
体積に変換してあげれば答えです。
\[
\mathrm{ 0.25mol \times \frac{22.4L} {1mol} = 5.6L}
\]
①③を行うパターンの問題でした。
(1)の0.50molから有効数字2桁と判断して6.0×1023を使いました。
練習問題
例題を通して、
基本的なmolの使い方は理解できたと思います。
ということで、
例題より少し難しい問題を練習問題として用意しました。
①まずはmolに直す
②化学反応などはmolで考える
③最後にmolから求めたい量に変換する
の基本を忘れずに、チャレンジしてみてください。
原子量はH=1、C=12、O=16、標準状態で有効数字は気にしなくてよい。
(1)水分子5.0×1024個は何gか。
(2)11.2Lの酸素は何gか。
(3)水素0.5gと酸素8gの混合気体の分子数は何個か。
(4)エチレン(C2H4)14gを完全燃焼させたときに生じる二酸化炭素(CO2)の体積は何Lか。
(1)水分子5.0×1024個は何gか。
まずはとにかくmolです。
\[
\mathrm{ 5.0×10^{24}個 \times \frac{1mol}{6.0\times 10^{23}個} = \frac{50}{6}mol}
\]
次にmolからgの変換では、分子量がわかればよかったですね。
H2O=18より、
\[
\mathrm{ \frac{50}{6}mol \times \frac{18g}{1mol} = 150g}
\]
よって150gが答えです。コップ1杯に5.0×10^{24}個もの分子が入っているんですね。
(2)11.2Lの酸素は何gか。
慣れてきた人は①と③を一気にやってもいいですよ。O2=32より、
\[
\mathrm{ 11.2L \times \frac{1mol}{22.4L} \times \frac{32g}{1mol}= 16g}
\]
次々と単位が約分されていきますね。
まだ慣れない人は順番にやってもいいです。
\begin{align*}
\mathrm{ 11.2L \times \frac{1mol}{22.4L}} &= \mathrm{0.50mol} \\
\mathrm{ 0.50mol \times \frac{32g}{1mol}} &= \mathrm{16g}
\end{align*}
以上から答えは16gです。
(3)水素0.5gと酸素8gの混合気体の分子数は何個か。
混合気体であっても順番に考えるだけです。
H2=2、O2=32より、
\begin{align*}
\mathrm{ 0.5g \times \frac{1mol}{2g} \times \frac{6.0\times 10^{23}個}{1mol}} &= \mathrm{1.5\times 10^{23}個} \\
\mathrm{ 8g \times \frac{1mol}{32g} \times \frac{6.0\times 10^{23}個}{1mol}} &= \mathrm{1.5\times 10^{23}個}
\end{align*}
よって合計の分子数は、
\[
1.5\times 10^{23}+1.5\times 10^{23}=3.0\times 10^{23}個
\]
となるので3.0×1023個です。
(4)エチレン(C2H4)14gを完全燃焼させたときに生じる二酸化炭素(CO2)の体積は何Lか。
最後の問題では化学反応が現れます。まだ習っていなければ飛ばしても大丈夫です。
まずはとにかくmolですね。
C2H4=28より、
\[
\mathrm{ 14g \times \frac{1mol}{28g} = 0.5mol}
\]
エチレン0.5molを材料に二酸化炭素を作ります。
そのレシピである化学反応式を書きましょう。
C2H4+3O2→2CO2+2H2O
エチレン1粒を材料として二酸化炭素が2粒できています。
よって二酸化炭素は0.5mol×2=1.0molできます。
以上から求める体積は、
\[
\mathrm{ 1.0mol \times \frac{22.4L}{1mol} = 22.4L}
\]
から22.4Lであるとわかります。
まとめ
今回は物質量(mol)の定義や考え方、
さらにはモル計算の練習をしました。
原子は1粒がとっても小さいから、
1箱に6.02×1023個詰め込んで考えよう、
というのが物質量でした。
物質量にさえ変換してしまえば、
そこからいろいろな化学量に変換できましたね。
モル計算は高校化学の第一の難関なので、
ぜひ繰り返し練習しておきましょう。














2)3.0×1024個の粒子は何molか。
これはmolに直すだけの問題なので
①を考えればいきなり答えになります。
3.0×1024個×1mol6.0×1023個=0.50mol
ここの計算は5.0molになると思うのですがどうですか。
ほんとですね、恥ずかしいミスをしてました…笑
ご指摘ありがとうございます、訂正しておきますー
練習の(3)の酸素の分子量は32じゃないですか?
ミスっちゃってますね、訂正しておきます。
ご指摘ありがとうございますm(__)m
練習問題の(3)はどうして最後答えが4.5×になるんですか?
コメントありがとうございます。
これは3.0の間違いですね…、混乱させてすいません。
記事修正の過程で意味不明なミスをしてました…。
記事の方は修正しておきましたm(__)m